Wenn sich eine Wirtschaft auf ihrer Transformationskurve befindet, kann sie die Produktion eines Gutes nur auf Kosten der Produktionsmenge des anderen Gutes erhöhen. Das Verhältnis der Zunahme des einen Gutes zur Abnahme des anderen Gutes heißt Grenzrate der Transformation. Grafisch erkennt man die Grenzrate der Transformation als Steigung der Transformationskurve.

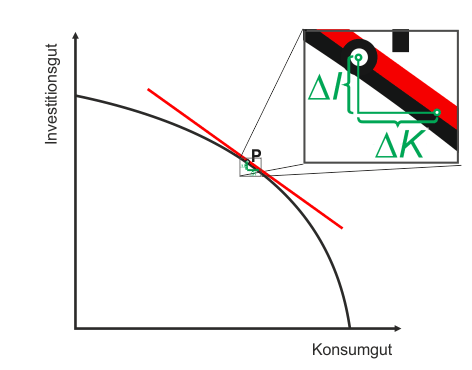
In der nebenstehenden Abbildung wird eine Wirtschaft betrachtet, die Investitionsgüter $I$ und Konsumgüter $K$ herstellen kann. Momenten soll sie sich in Punkt P befinden. Solange wir relativ zu den Ausgangsmengen nur kleine Änderungen der Produktionsmengen von $I$ und $K$ in der Nähe des Punktes P betrachten, macht es keinen großen Unterschied, ob wir uns auf der schwarzen Transformationskurve selbst oder auf der roten Tangente bewegen, die in Punkt P an die Transformationskurve angelegt ist. Damit Sie die kleinen Änderungen erkennen können, ist der Bereich um P im Ausschnitt vergrößert dargestellt.

Wenn die Einwohner in unserer Wirtschaft ("die Gesellschaft") ausgehend von der Situation P die Produktion der Konsumgüter um $\Delta K$ erhöhen wollen, dann kostet das einen Verzicht in Höhe von $\Delta I$ Einheiten an Investitionsgütern. Das Verhältnis von$\Delta I$ zu $\Delta K$ stimmt überein mit der Steigung der roten Tangente. Diese stimmt wiederum mit der Steigung der Transformationskurve in Punkt P überein. Also können wir feststellen, dass in der Nähe von P die Opportunitätskosten für $\Delta K$ Einheiten mehr Konsum $\Delta I$ Einheiten weniger Investitionen betragen. Allgemeiner formuliert:

Mit Hilfe der Grenzrate der Transformation lässt sich bestimmen, was eine weitere Konsumgütereinheit kostet. Zwar lässt sich kein absoluter Preis in einer Währungseinheit angeben, aber immerhin lässt sich sagen, dass ein $K$ einen Preis von $\frac{\Delta I} {\Delta K}$ hat. Betrüge $\Delta I = 20$ und $\Delta K = 10$, dann kostete eine Einheit Konsumgut zwei Einheiten Investitionsgüter.

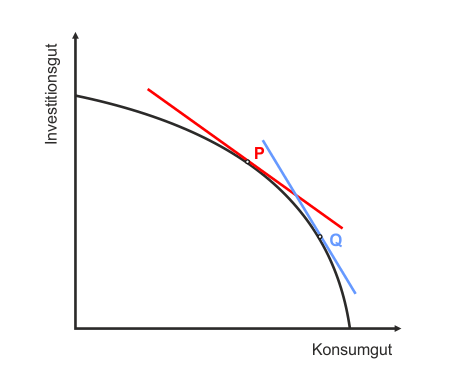
Das Preisverhältnis ändert sich auf der Transformationskurve. Bewegen wir uns zum Beispiel von Punkt P zum Punkt Q, wird das Konsumgut (gemessen in Einheiten des Investitionsgutes) teurer. Um das zu erkennen, reicht es aus, die Steigungen der Transformationskurve in P und zu Q zu vergleichen. Je steiler die Transformationskurve verläuft, um so mehr Investitionsgüter muss die Gesellschaft für eine zusätzliche Einheit des Konsumguts aufgeben.

Beim angenommenen Verlauf der Transformationskurve werden Konsumgüter umso teurer, je mehr von ihnen hergestellt werden. Das gilt auch für die Investitionsgüter: Je mehr von ihnen hergestellt werden, desto teurer werden sie (gemessen in Konsumgütereinheiten). Dieses Phänomen hat einen Namen: "Gesetz von den steigenden Opportunitätskosten". Ob das Gesetz gilt oder nicht, hängt offensichtlich vom Verlauf der Transformationskurve, also letztendlich von der Technik ab, mit der die Güter hergestellt werden. Bei einem durchgängig konkaven Verlauf (so wie hier; die Tangenten in beliebigen Punkten wie P und Q verlaufen immer oberhalb der Transformationskurve) gilt das Gesetz ohne Einschränkung. Möchte man also die Gründe in Erfahrung bringen, unter welchen Umständen das Gesetz gilt, müsste man erkunden, welche Umstände im Detail für einen konkaven Verlauf der Transformationskurve verantwortlich sind.

Hier beschränken wir uns auf Plausibilitätsüberlegungen: Wir betrachten weiterhin zwei Güter. Das eine Gut sei "saubere Luft", das andere Gut sein ein "Warenkorb", der alle anderen Güter repräsentiert (bspw. Butter, Fernseher, Autos, Schienen, Gesundheit, Urlaub, Zahnprothesen ... - alle erdenklichen Güter). Wir lassen Experten ein Maß für die Sauberkeit der Luft konstruieren, das auf das Intervall [0, 100] skaliert wird. Dabei soll 0 bedeuten, dass jedes Leben erlischt, und 100 stehe für absolut reine Luft.

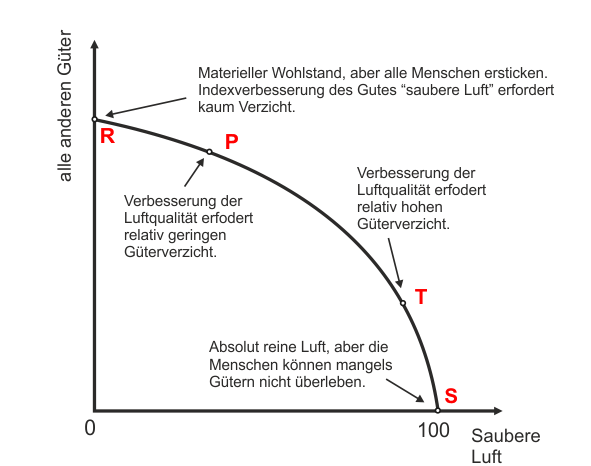
Die Situation, in der wir uns jetzt gerade befinden, sei gekennzeichnet durch einen Indexwert für saubere Luft von 50. Dann bedarf es vermutlich keiner allzu großen Anstrengungen, ihn auf 51 zu steigern. Wir würden natürlich mit den Maßnahmen beginnen, die günstig durchgeführt werden könnten. Vermutlich gäbe es schon hier heftigen politischen Streit: Mehr Atomkraft, um Kohlekraftwerke zu ersetzen? Umweltzonen einrichten? Fahrverbote bei hoher Feinstaubbelastung? Staubfilter für Kamine? Verbot älterer Heizungen usw. usw.

Gehen wir davon aus, es könnte immer Einigkeit über die erforderlichen Maßnahmen erzielt werden und die Sauberkeit der Luft stiege und stiege und stiege. Das würde ohne Frage damit einhergehen, dass wir zu immer strengeren Maßnahmen greifen müssten, was zu erheblichen Einschränkungen im täglichen Leben führen würde. Verbrennungsmotoren würden verboten, Strom- und Öl- und Gasverbrauch wären streng rationiert, das Verbrennen von Gartenabfällen wäre mit drakonischen Strafen belegt.

Allgemein lässt sich dies wie folgt zusammenfassen:

Diese Aussage wird auch das "Gesetz vom abnehmenden Ertragszuwachs" genannt. Somit lässt sich alternativ formulieren:

Ein zweiter Grund für die Konkavität der Transformationskurve sind unterschiedliche Kapitalintensitäten in der Herstellung der Güter. Für eine Erklärung sei unterstellt, die Wirtschaft stelle Investitions- und Konsumgüter her. Die Produktion von Investitionsgütern erfordere im Vergleich zur Herstellung von Konsumgütern einen relativ hohen Kapitaleinsatz. Unter den Konsumgütern ist der Dienstleistungsanteil hoch. Dienstleistungen werden arbeitsintensiv produziert. Im Vergleich zu den Investitionsgütern ist der Arbeitseinsatz also relativ hoch, der Kapitaleinsatz dagegen relativ gering.

Wir nehmen konkret an, dass Investitionsgüter sich (bei gegebenen Faktorpreisen) zu geringstmöglichen Kosten herstellen lassen, wenn in der Produktion je zwei Maschinen (Kapital $K$) und eine Arbeitskraft ($L$) eingesetzt werden. Bei den Konsumgütern sei es genau umgekehrt: Für eine kostengünstige Produktion sei ein Faktormix von einer Maschine und zwei Arbeitskräften optimal. Unsere Wirtschaft verfüge über $K = 60$ Maschinen und $L = 60$ Arbeitskräfte.

Wenn sowohl Investitions- als auch Konsumgüter hergestellt werden, ist es ohne Weiteres möglich, beide Produktionen mit der optimalen Kapitalintensität zu fahren. Es könnten 40 Maschinen und 20 Arbeitskräfte in der Investitionsgüterproduktion eingesetzt werden. Dann betrüge die Kapitalintensität in diesem Sektor 2 ($= \frac{40K}{20L}$). Werden die verbleibenden Faktoren in der Konsumgüterindustrie eingesetzt, ist die Kapitalintensität mit 0,5 ($= \frac{20K}{40L}$) dort ebenfalls optimal.

Diese optimalen Kapitalintensitäten in den Sektoren lassen sich aber nicht aufrecht erhalten, wenn sich die Gesellschaft mehr Konsumgüter wünscht. Angenommen, die Bevölkerung fiele in einen wahren Konsumrausch und verabschiede sich vollkommen von der Investitionsgüterproduktion (es wird nicht mehr gespart. Sie beschäftigte also alle Produktionsfaktoren in der Konsumgüterbranche. Dadurch stiege die Kapitalintensität in dieser Branche auf 1 ($= \frac{60K}{60L}$). Die optimale Kapitalintensität kann nicht aufrecht erhalten werden, wenn sich die Wirtschaft mehr und mehr auf ein Produkt spezialisiert. Je weiter man sich aber von der optimalen Kapitalintensität entfernt, desto teuer wird die Produktion. Fazit:

Das Gesetz steigender Opportunitätskosten kann mit unterschiedlich kapitalintensiven Produktionen begründet werden.

Hier finden Sie ein fortgeschrittenes Zahlenbeispiel, das deutlicht macht, wie es trotz linear homogener Produktionsfunktionen ("lineare Technologie") durch unterschiedliche Kapitalintensitäten in der Herstellung zu konkaven Transformationskurven kommen kann: Konkave Transformationskurve bei linear homogenen Produktionsfunktionen.